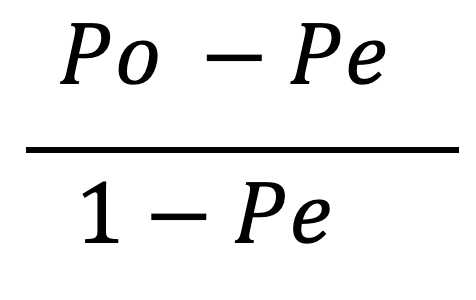(This is a crosspost from the official Surge AI blog, where we're building the greatest source of NLP content. If you need help with data labeling and NLP, say hello!)
Introduction
Imagine you're a Harvard professor teaching English 101. You’re tired of grading homework and want to get back to your research, so you decide to build an NLP model that can score your students' essays as a Pass or Fail for you.
In order to build a training dataset, you use a workforce of data labelers to read and grade your essays. Of course, you want to ensure that every rater applies the grading rubric consistently: if two raters read the same 10 essays, for example, you want to ensure that each essay receives a similar grade from both of them. Otherwise, your training data may be too noisy and subjective to be of much use! So how can you measure rater consistency?
One candidate is Cohen’s kappa statistic, which measures how often two raters agree with each other after accounting for the likelihood they’d agree by chance. In this post, we’ll explain how Cohen's kappa uncovers disagreements between raters that are obscured by simpler metrics like percentage agreement.
A mystery
As starving aspiring novelists, Alix and Bob were both happy to moonlight as data labelers grading student essays. Wanting to be fair to the students, they tracked how often they agreed whether to pass or fail a particular student, and found their judgements matched 90% of the time. A week in, though, Bob was shocked to discover that he was getting twice as many complaints from flunked students as Alix. How could there be such a huge difference if their decisions were so similar?
The problem with simple measures of inter-rater reliability, like the percentage of samples both raters label identically, is that they don’t account for the likelihood that two people would agree by random chance. To understand how this works, let’s consider the confusion matrix for the 100 essays Alix and Bob graded in their first week:
This is clearly a talented bunch of students, because 86% earned passes from both raters. The raters also rarely disagreed about which essays were good: if Alix passed a student, Bob did too 86 / 94 = 91% of the time. Things are different when we look at the 14% of the students who failed. If Bob failed a student, Alice failed the same student only 4 / 12 = 33% of the time, and overall Bob failed twice as many students as Alix (12 vs. 6).
Because the student essay data is imbalanced, with far more students passing than failing, we have two problems:
- Even though all the raters seem superficially similar, some of them are actually twice as strict as others, which isn’t fair to the students.
- We can’t tell whether some of our raters are slacking off by just passing every essay, knowing the high overall pass rate will mean their judgments don’t look too different from the diligent raters.
We can fix both these issues by using Cohen’s kappa to measure inter-rater reliability. This metric subtracts the probability that two raters would agree if they were guessing randomly from the probability they actually agreed.
Calculating Cohen’s kappa
The formula for Cohen’s kappa is:
Po is the accuracy, or the proportion of time the two raters assigned the same label. It’s calculated as (TP+TN)/N:
TP is the number of true positives, i.e. the number of students Alix and Bob both passed. TN is the number of true negatives, i.e. the number of students Alix and Bob both failed. N is the total number of samples, i.e. the number of essays both people graded. Plugging in the values from the example above, we get Po = (86 + 4)/100= 0.9.
Pe is the probability that both raters would choose the same label if they both just guessed randomly. It’s the sum of two terms: P₁ is the probability both raters randomly choose the first label (pass), and P₂ is the probability they both choose the second label (fail). These probabilities can be calculated using the count of true positive and true negative described above plus two additional terms:
FN is the number of false negatives. In this case, it’s not clear which, if any, rater is objectively correct, so we can arbitrarily define this as the number of students Alix passed and Bob failed. FP is the number of false positives, i.e. the number of students Bob passed and Alix failed. Now we can use the following formulas to find P₁ and P₂:
For the example above, Pe = .827 + .007 = .834. We can plug this result into the formula for Cohen’s kappa to get:
So what does this value mean?
Interpreting Cohen’s kappa
Cohen’s kappa ranges from 1, representing perfect agreement between raters, to -1, meaning the raters choose different labels for every sample. A value of 0 means the raters agreed exactly as often as if they were both randomly guessing.
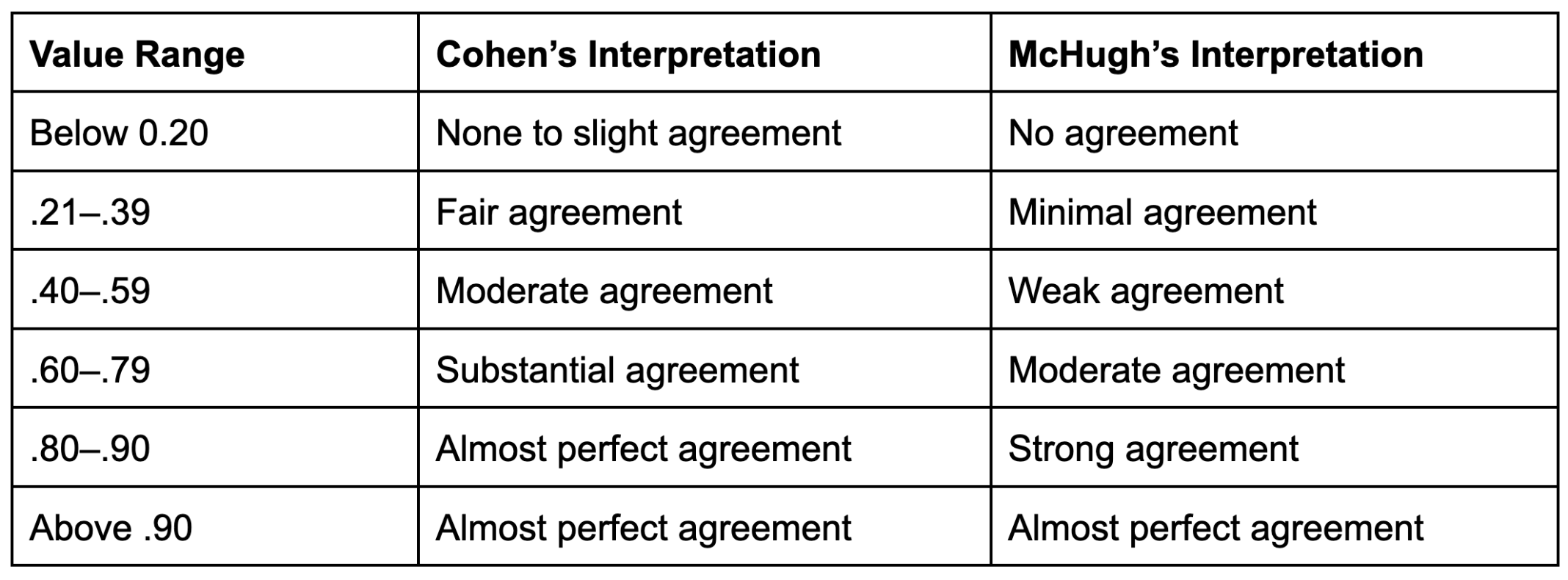
In this case, it’s pretty clear that while Alix and Bob are agreeing more often than random chance, their grading philosophies aren’t very similar. However, there’s still substantial debate about what kappa-value cutoffs to use for subjective labels like “strong” agreement. As the table below shows, Jacob Cohen’s original descriptive categories would classify Alix and Bob as “moderately” in agreement, but they’re only “weakly” in agreement according to Mary McHugh’s stricter thresholds intended for use in healthcare research:
It’s important to remember that there’s a difference between consistent raters and high-quality raters. Alix and Bob could easily achieve a Cohen’s kappa of 1 if they were both so lazy they decided to just auto-pass every single essay. A high Cohen’s kappa might also reflect shared inappropriate biases - imagine if Alix and Bob both resented being forced to read Shakespeare in high school and automatically failed anyone who mentioned him.
Similarly, negative values for Cohen’s kappa don’t automatically mean that one of the raters is low-quality. They might just have different values or interpretations of the labeling criteria. In this essay grading example, for instance, Alix might value thoroughness while Bob prefers students who are concise. In that case, Alix would preferentially fail the short essays Bob thought were the best written, and vice versa with the long essays. Pairs of raters with negative Cohen’s kappas can actually be valuable in tasks where representing a wide variety of viewpoints is important. Even for tasks that require consistency, low Cohen’s kappa values may reflect ambiguous instructions or inherently subjective questions (what makes an essay good anyway?) rather than rater error.
Cohen’s kappa in a nutshell
Pros
- Good for measuring agreement about datasets that are imbalanced or otherwise allow a high accuracy rate with random guessing.
- Can be easily adapted to measure agreement about more than two labels. (For example, if Alix and Bob gave every essay an A-F grade instead of just pass/fail.)
- Negative scores can be used to identify raters with diverse viewpoints.
Cons
- Can only compare two raters, not three or more. (Unlike next week's spotlight metric, Fleiss’ kappa!)
- Not intuitively clear what a given value means, unlike a simpler metric like percentage agreement.
- Debate over meaningful thresholds for “weak” vs. “moderate” vs. “strong” agreement.
- Read more about the pitfalls of inter-reliability metrics in our previous post in this series!
In future posts, we'll dive more into other inter-rater reliability metrics and their advantages compared to Cohen's kappa.
Surge AI is a data labeling workforce and platform that provides world-class data to top AI companies and researchers. We're built from the ground up to tackle the extraordinary challenges of natural language understanding — with an elite data labeling workforce, stunning quality, rich labeling tools, and modern APIs. Want to improve your model with context-sensitive data and domain-expert labelers? Schedule a demo with our team today!